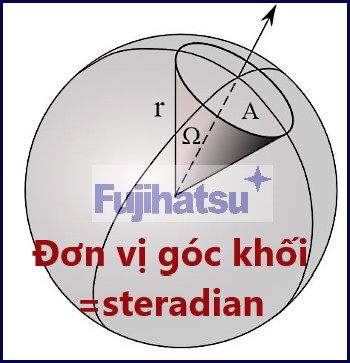
Đơn vị đo góc khối là gì?

   Góc khối là góc được tạo trong không gian ba chiều mà một vật thể phụ thuộc vào một điểm. Góc khối là thước đo mức độ lớn của một vật thể đối với người quan sát khi nhìn từ điểm đó. Biểu tượng cho góc khối là Ω (chữ Hy Lạp omega).

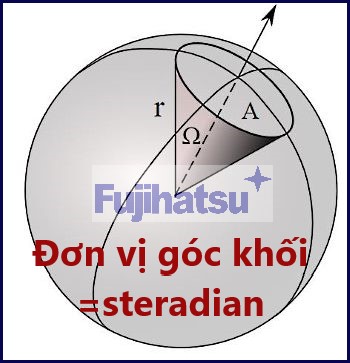
Ảnh: minh họa (Internet)

   Một góc khối có thể được định nghĩa theo một khu vực trên bề mặt của một hình cầu được căn giữa ở đỉnh của góc. Điều này tương đương với việc xác định một góc phẳng theo chiều dài của cung trên một vòng tròn phụ thuộc vào tâm. Góc khối cũng có thể được định nghĩa là một góc được tạo bởi ba hoặc nhiều mặt phẳng cắt nhau tại một điểm chung (đỉnh). Đơn vị theo hệ thống đo lường quốc tế (SI) của góc khối là steradian (sr). Góc khối của một hình cầu hoàn chỉnh là 4π sr (bốn pi steradian). 
Góc khối tương ứng với mặt của khối lập phương được đo tại tâm = 2π / 3 sr
1 steradian = (180 / π) ² độ vuông.

Khái niệm về một góc độ vững chắc và thuật ngữ steradian có thể gây bối rối cho những người chỉ làm quen với các góc độ thông thường. Mọi người đều biết góc 90 ° trông như thế nào và thậm chí đề cập đến nó như là rad / 2 radian là tương đối dễ hiểu. Nhưng đó là một vấn đề khác hoàn toàn với các góc vững chắc vì nó phải được tưởng tượng trong không gian ba chiều mà không có một tài liệu tham khảo rõ ràng.

Đầu tiên chúng ta hãy xem xét một vòng tròn tham chiếu và một góc bình thường. Góc cũng có thể được giải thích dưới dạng cung. Gọi s là độ dài của cung và r là bán kính của đường tròn. 
   Góc thông thường tính bằng radian được cho bởi θ = (s / r)
   Tính bằng độ, nó được định nghĩa là = (360 / 2π) (s / r) 

Bây giờ giả sử một hình nón giao với hình cầu bán kính R. Coi S là diện tích bề mặt được phụ thuộc bởi giao điểm của hình cầu và hình nón. Độ lớn của góc khối được xác định bằng tỷ lệ giữa diện tích S của hình chiếu vật thể lên một hình cầu có tâm là điểm quan sát với bình phương bán kính R của hình cầu đó:
Góc khối được xác định = (S / r²)

Nếu bề mặt bao phủ toàn bộ quả cầu thì số lượng là 4π. Nếu bạn biết góc khối Ω trong vô cực thì bạn có thể dễ dàng tính diện tích tương ứng của bề mặt của bất kỳ hình cầu nào từ biểu thức S = R ² , trong đó R là bán kính của hình cầu.

Các ứng dụng thực tế của các góc khối bao gồm định nghĩa độ chói và cường độ sáng và đạo hàm của định luật Gauss. Nó cũng được sử dụng trong mô hình toán học trong Phương pháp phần tử ranh giới để tính toán tiềm năng. Các góc khối là cần thiết để xác định kích thước của phối tử trong các phức kim loại và để tính toán cường độ của từ trường và điện trường cho một phân bố điện tích cho trước.

Mặt trời và Mặt trăng có cùng kích thước rõ ràng khi nhìn từ trái đất. Chúng chiếm diện tích 0,001% của bán cầu thiên thể, tương đương với một góc khối xấp xỉ 6 × 10 ^-5 Steradian.
Nguồn: calculator.org
Bài viết liên quan:
1/ Đơn Vị Đo Góc Là Gì? (Giải Thích Đơn Giản Nhất)
http://fujihatsu.com/don-vi-do-goc-la-gi-giai-thich-don-gian-nhat-1-2-186931.html
2/ Đơn Vị Đo Khối Lượng Nguyên Tử Là Gì?
http://fujihatsu.com/don-vi-do-khoi-luong-nguyen-tu-la-gi-1-2-186929.html