Khi nói đến vũ trụ, con người chúng ta thích những thứ quen thuộc. Khi kiểm tra các ngoại hành tinh, chúng tôi phân loại chúng dựa trên sự tương đồng của chúng với các hành tinh trong Hệ Mặt trời của chúng ta - tức là trên mặt đất, khí quyển, kích thước Trái đất, cỡ sao Mộc, cỡ sao Hải Vương, v.v. Và khi đo khoảng cách thiên văn, chúng ta làm được nhiều tương tự.
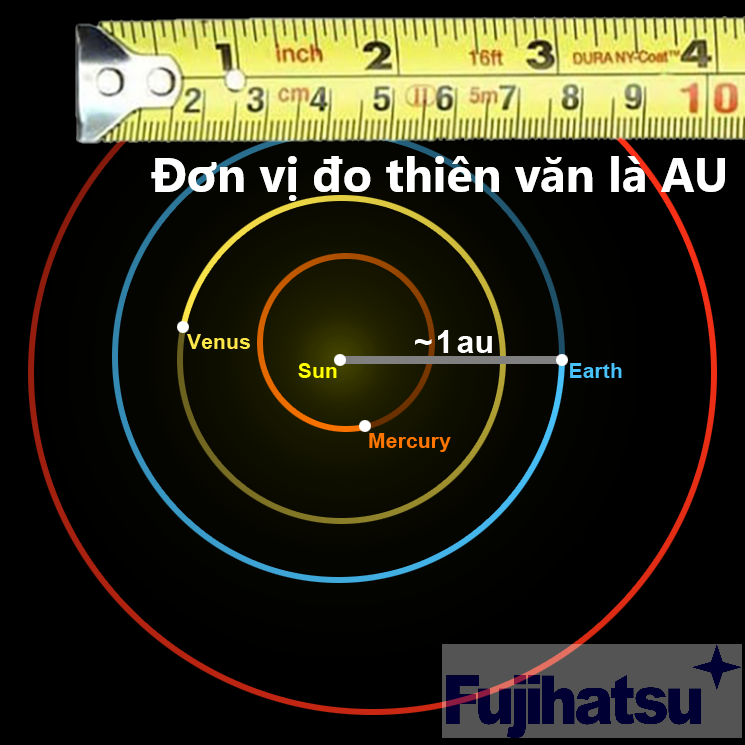
Chẳng hạn, một trong những phương tiện được sử dụng phổ biến nhất để đo khoảng cách trong không gian được gọi là Đơn vị Thiên văn (AU). Dựa trên khoảng cách giữa Trái đất và Mặt trời, đơn vị này cho phép các nhà thiên văn học mô tả khoảng cách rộng lớn giữa các hành tinh Mặt trời và Mặt trời, và giữa các hành tinh ngoài mặt trời và các ngôi sao của họ.
Định nghĩa:
Theo quy ước thiên văn hiện nay, một đơn vị thiên văn duy nhất là tương đương với 149,597,870.7 kilômét (hoặc 92.955.807 dặm). Tuy nhiên, đây là khoảng cách trung bình giữa Trái đất và Mặt trời, vì khoảng cách đó có thể thay đổi trong thời kỳ quỹ đạo của Trái đất. Nói cách khác, khoảng cách giữa Trái đất và Mặt trời thay đổi trong một năm.

Trong suốt một năm, Trái đất đi từ khoảng cách 147.095.000 km (91.401.000 dặm) từ Mặt trời tại perihelion (điểm gần nhất của nó) đến 152.100.000 km (94.500.000 dặm) tại aphelion (điểm xa nhất của nó) - hoặc từ khoảng cách 0,983 AU đến 1.016 AU.
Lịch sử phát triển:
Ví dụ được ghi lại sớm nhất của các nhà thiên văn học ước tính khoảng cách giữa Trái đất và Mặt trời bắt nguồn từ Cổ vật Cổ điển. Trong công trình BCE thế kỷ thứ 3, Về kích thước và khoảng cách của mặt trời và mặt trăng - được cho là của nhà toán học Hy Lạp Aristarchus of Samos - khoảng cách được ước tính là từ 18 đến 20 lần khoảng cách giữa Trái đất và Mặt trăng .
Tuy nhiên, Archimedes đương đại của ông, trong tác phẩm BCE thế kỷ thứ 3 của ông , Sandreckoner , cũng tuyên bố rằng Aristarchus of Samos đã đặt khoảng cách gấp 10.000 lần bán kính Trái đất. Tùy thuộc vào các giá trị cho một trong hai ước tính, Aristarchus bị tắt bởi hệ số khoảng 2 (trong trường hợp bán kính Trái đất) đến 20 (khoảng cách giữa Trái đất và Mặt trăng).
Văn bản toán học lâu đời nhất của Trung Quốc - chuyên luận BCE thế kỷ 1 được gọi là Zhoubi Suanjing - cũng chứa một ước tính về khoảng cách giữa Trái đất và Mặt trời. Theo chuyên luận nặc danh, khoảng cách có thể được tính bằng cách tiến hành các phép đo hình học về độ dài của bóng tối không được tạo bởi các vật thể cách nhau ở khoảng cách cụ thể. Tuy nhiên, các tính toán dựa trên ý tưởng Trái đất phẳng.

Nhà toán học và thiên văn học nổi tiếng thế kỷ thứ 2 Ptolemy đã dựa vào các phép tính lượng giác để đưa ra ước tính khoảng cách tương đương với 1210 lần bán kính Trái đất. Sử dụng các ghi chép về nhật thực, ông ước tính đường kính rõ ràng của Mặt trăng, cũng như đường kính rõ ràng của hình nón của Trái đất đi ngang qua Mặt trăng trong nguyệt thực.
Sử dụng thị sai của Mặt trăng, ông cũng đã tính toán kích thước rõ ràng của Mặt trời và Mặt trăng và kết luận rằng đường kính của Mặt trời bằng với đường kính của Mặt trăng khi mặt sau ở khoảng cách lớn nhất so với Trái đất. Từ đó, Ptolemy đạt được tỷ lệ của mặt trời với khoảng cách mặt trăng xấp xỉ 19 đến 1, con số tương tự của Aristarchus.
Trong một nghìn năm tới, các ước tính của Ptolemy về khoảng cách Trái đất-Mặt trời (giống như hầu hết các giáo lý thiên văn học của ông) sẽ vẫn còn nguyên tắc giữa các nhà thiên văn học châu Âu và Hồi giáo thời trung cổ. Mãi đến thế kỷ 17, các nhà thiên văn học mới bắt đầu xem xét lại và xem xét lại các tính toán của mình.
Điều này được thực hiện nhờ vào việc phát minh ra kính viễn vọng, cũng như Ba định luật về chuyển động hành tinh của Kepler , giúp các nhà thiên văn tính toán khoảng cách tương đối giữa các hành tinh và Mặt trời với độ chính xác cao hơn. Bằng cách đo khoảng cách giữa Trái đất và các hành tinh Mặt trời khác, các nhà thiên văn học đã có thể tiến hành các phép đo thị sai để thu được các giá trị chính xác hơn.

Đến thế kỷ 19, các quyết định về tốc độ ánh sáng và hằng số quang sai của ánh sáng đã dẫn đến phép đo trực tiếp đầu tiên về khoảng cách Trái đất-Mặt trời tính bằng km. Đến năm 1903, thuật ngữ đơn vị thiên văn học đầu tiên đã được sử dụng lần đầu tiên. Và trong suốt thế kỷ 20, các phép đo ngày càng chính xác và tinh vi, một phần nhờ vào những quan sát chính xác về tác động của Thuyết tương đối của Einstein .
Cách sử dụng hiện đại:
Đến thập niên 1960, sự phát triển của các phép đo radar trực tiếp, đo từ xa và thăm dò Hệ mặt trời với các đầu dò không gian đã dẫn đến các phép đo chính xác về vị trí của các hành tinh bên trong và các vật thể khác. Năm 1976, Liên minh Thiên văn Quốc tế (IAU) đã thông qua một định nghĩa mới trong Đại hội đồng lần thứ 16 của họ . Là một phần của Hệ thống các hằng số thiên văn của họ , định nghĩa mới đã nêu:
Để đáp ứng với sự phát triển của các phép đo siêu chính xác, Ủy ban Trọng lượng và Đo lường (CIPM) quốc tế đã quyết định sửa đổi Hệ thống Đơn vị Quốc tế (SI) vào năm 1983. Phù hợp với điều này, họ đã xác định lại máy đo được đo theo tốc độ ánh sáng trong chân không.

Tuy nhiên, đến năm 2012, IAU xác định rằng sự cân bằng của thuyết tương đối làm cho phép đo AU quá phức tạp và xác định lại đơn vị thiên văn theo mét. Theo quy định này, một AU duy nhất là tương đương với 149.597.870,7 km chính xác ( 92,955807 triệu dặm), 499 light-giây, 4,8481368 × 10 -6 của một parsec, hoặc 15,812507 × 10 -6 của một năm ánh sáng.
Ngày nay, AU được sử dụng phổ biến để đo khoảng cách và tạo các mô hình số cho Hệ Mặt Trời. Nó cũng được sử dụng khi đo các hệ mặt trời ngoài trời, tính toán mức độ của các đám mây hình thành hành tinh hoặc khoảng cách giữa các hành tinh ngoài mặt trời và ngôi sao mẹ của chúng. Khi đo khoảng cách giữa các vì sao, AU quá nhỏ để cung cấp các phép đo thuận tiện. Do đó, các đơn vị khác - chẳng hạn như Parsec và năm ánh sáng - được dựa vào.
Vũ trụ là một nơi rộng lớn và đo lường ngay cả góc nhỏ của chúng ta tạo ra một số kết quả đáng kinh ngạc. Nhưng như mọi khi, chúng tôi muốn thể hiện chúng theo những cách dễ hiểu và quen thuộc.
Nguồn: universetoday
Bài viết liên quan:
1/Đơn Vị Đo Chiều Dài Lớn Nhất?
http://fujihatsu.com/don-vi-do-chieu-dai-lon-nhat-1-2-186763.html
2/1 Hải Lý Bằng Bao Nhiêu Km?
http://fujihatsu.com/1-hai-ly-bang-bao-nhieu-km-1-2-186735.html